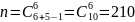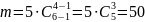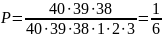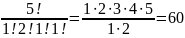Задачи на вероятность номер телефона

Решения задач на классическое определение вероятности

Онлайн-калькуляторы с примерами

Хотите научиться решать типовые задачи на эту тему? Используйте статьи-инструкции-калькуляторы:

• Задача про шары (в урне находится $k$ белых и $n$ черных шаров, вынимают $m$ шаров…)
• Задача про детали (в ящике находится $k$ стандартных и $n$ бракованных деталей, вынимают $m$ деталей…)
• Задача про лотерейные билеты (в лотерее участвуют $k$ выигрышных и $n$ безвыигрышных билета, куплено $m$ билетов…)
• Вычисление вероятности: подбрасывания монеты
• Вычисление вероятности: подбрасывание игральных костей

Решенные задачи

Задача 1. Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.

Задача 2. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.

Задача 3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.

Задача 4. На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую?

Задача 5. Шесть рукописей случайно раскладывают по пяти папкам. Какова вероятность того, что ровно одна папка останется пустой?

Задача 6. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.

Задача 7. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.

Задача 8. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «юрта».

Задача 9. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово «кукла»?

Задача 10. В пачке 20 перфокарт, помеченных номерами 101, 102, … , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.

Задача 11. Пятитомное собрание сочинений расположено на полке в случайном порядке. Какова вероятность того, что книги стоят слева направо в порядке нумерации томов (от 1 до 5)?

Задача 12. Случайно выбранная кость в игре домино оказалась не дублем. Найти вероятность того, что вторую также взятую наудачу кость домино можно приставить к первой.

Задача 13. Бросаются две игральные кости. Определить вероятность того, что: а) сумма числа очков не превосходит N; б) произведение числа очков не превосходит N; в) произведение числа очков делится на N.
N=8

Решебник по теории вероятностей

Срочно нужно решение задачи? Более 11000 полностью оформленных задач (в том числе 2300+ задач на классическое определение вероятности):

Рассмотрим случайный телефонный номер. Какова вероятность того, что среди трех последних цифр этого номера хотя бы две цифры одинаковы?

---

Решение

Согласно классическому определению вероятностей имеем формулу (displaystyle P(A)=frac{m}{n}), где (m) – число благоприятных исходов (в нашем случае хотя бы две цифры номера одинаковы), а (n) – количество всех исходов (всего номеров).

Всего возможно комбинаций из трех цифр (10^3=1000).

Найдем количество номеров с разными числами. На первое место можно поставить любое число (всего у нас чисел (10)), значит на второе место уже можно поставить всего (10-1=9) чисел, а на третьем месте уже остается (10-1-1=8) чисел. Значит, номеров с разными числами (10cdot 9cdot 8=720).

Отсюда, номеров, где хотя бы две цифры совпадает будет равно (1000-720=280).

Подставим в формулу и найдем вероятность того, что среди трех последних цифр этого номера хотя бы две цифры одинаковы: ( displaystyle P(A)=frac{280}{1000}=0,28).

Ответ: (0,28).

---

Источник: ЕГЭ 2023 Математика. Профильный уровень. Типовые экзаменационные варианты. 36 вариантов (вариант 10) (Купить книгу)

Задачи на классическое определение вероятности

Задача
1. Абонент
забыл последнюю цифру номера телефона
и поэтому набирает её наугад. Определить
вероятность того, что ему придётся
звонить не более чем в 3 места.

Решение: Вероятность
набрать верную цифру из десяти равна
по условию 1/10. Рассмотрим следующие случаи: 

1.
первый звонок оказался верным, вероятность
равна 1/10 (сразу набрана нужная цифра).

2.
первый звонок оказался неверным, а
второй — верным, вероятность равна
9/10*1/9=1/10 (первый раз набрана неверная
цифра, а второй раз верная из
оставшихся девяти цифр).

3.
первый и второй звонки оказались
неверными, а третий — верным, вероятность
равна 9/10*8/9*1/8=1/10 (аналогично пункту 2). 

Всего
получаем P=1/10+1/10+1/10=3/10=0,3 — вероятность
того, что ему придется
звонить не более чем в три места. 

Ответ: 0,3

Задача
2. Абонент
забыл последние 2 цифры телефонного
номера, но помнит, что они различны и
образуют двузначное число, меньшее 30.
С учетом этого он набирает наугад 2
цифры. Найти вероятность того, что это
будут нужные цифры.

Решение: Используем
классическое определение вероятности:
P=m/n, где n — число всех возможных элементарных
исходов, m — число элементарных исходов,
благоприятствующих осуществлению
события. 

m
= 1, так как только одно число правильное.
Подсчитаем количество всех возможных
двузначных чисел с разными цифрами,
меньшее 30, которые может набрать абонент:

10	12	13	14	15	16	17	18	19
20	21	23	24	25	26	27	28	29

Таких чисел n = 18 штук. Тогда искомая вероятность P=1/18. 

Ответ: 1/18.

Задача
3. Шесть
шаров случайным образом раскладывают
в три ящика. Найти вероятность того, что
во всех ящиках окажется разное число
шаров, при условии, что все ящики не
пустые.

Решение: Используем
классическое определение вероятности:
P=m/n, где m — число исходов, благоприятствующих
осуществлению события, а n — число всех
возможных исходов. 

m
= 6, так как есть только три случая
расположения 6 шаров по 3 ящикам, чтобы
во всех ящиках оказалось разное число
шаров: (1, 2, 3), (2, 1, 3), (3, 2, 1), (1, 3, 2), (2, 3, 1),
(3, 1, 2). Всего случаев расположения 6 шаров
по 3 ящикам, чтобы ни один
ящик не остался пустым равно 
 

Тогда
искомая вероятность P=6/10. 

Ответ: 0,6.

Задача
4. На
шахматную доску случайным образом
поставлены две ладьи. Какова вероятность,
что они не будут бить одна другую?

Решение: Используем
классическое определение вероятности:
P=m/n, где m — число исходов, благоприятствующих
осуществлению события, а n — число всех
возможных исходов. 

Число
всех способов расставить ладьи равно
n = 64*63 (первую ладью ставим на любую из
64 клеток, а вторую — на любую из оставшихся
63 клеток). Число способов расставить
ладьи так, что они не будут бить одна
другую равно m = 64*(64-15) =
64*49. 

Тогда искомая вероятность P=(64*49)/(64*63)=49/63. 

Ответ: 49/63.

Задача
5. Шесть
рукописей случайно раскладывают по
пяти папкам. Какова вероятность того,
что ровно одна папка останется пустой?

Решение: Используем
классическое определение вероятности:
P=m/n, где m — число исходов, благоприятствующих
осуществлению события, а n — число всех
возможных исходов. 

Подсчитаем

  —
число различных способов разложить 6
рукописей по 5 папкам, причем в каждой
папке может быть любое количество
рукописей. Теперь подсчитаем
 —
число способов разложить 6 рукописей
по 4 папкам, причем в каждой папке должно
быть не менее одной рукописи. При этом
нужно полученное число сочетаний
умножить на 5, так как папку, которая
останется пустой, можно выбрать 5
способами. Искомая вероятность
Р=50/210=5/21. 

Ответ: 5/21.

Задача
6. Цифры
1, 2, 3, …, 9, выписанные на отдельные
карточки складывают в ящик и тщательно
перемешивают. Наугад вынимают одну
карточку. Найти вероятность того, что
число, написанное на этой карточке: а)
четное; б) двузначное.

Решение: Используем
классическое определение вероятности:
P=m/n, где n — число всех возможных элементарных
исходов, m — число элементарных исходов,
благоприятствующих осуществлению
события.

Случай
а). n = 9, так как всего 9 различных карточек.
m = 4, так как всего на 4 карточках
написаны четные числа (2, 4, 6, 8). Тогда P=4/9.

Случай
б). n = 9, так как всего 9 различных карточек.
m = 0, так как на всех карточках
написаны однозначные числа. Тогда P=0/9=0. 

Ответ: 4/9,
0.

Задача
7. На
полке в случайном порядке расставлено
40 книг, среди которых находится трехтомник
Пушкина. Найти вероятность того, что
эти тома стоят в порядке возрастания
номера слева направо, но не обязательно
рядом.

Решение: Используем
классическое определение вероятности:
P=m/n, где n — число всех возможных элементарных
исходов, m — число элементарных исходов,
благоприятствующих осуществлению
события (Тома стоят в порядке возвозрастания
номера слева направо, но не обязательно
рядом). 

n
= 40*39*38, так как первый том можно поставить
на любое из 40 мест, второй — на любое из
39 мест и третий — на любое из оставшихся
38 мест. 

Тогда искомая вероятность  
 

Ответ: 1/6.

Задача
8. На
каждой из пяти одинаковых карточек
напечатана одна из следующих букв: «а»,
«м», «р», «т», «ю».
Карточки тщательно перемешаны. Найти
вероятность того, что на четырех вынутых
по одной карточке можно прочесть слово
«юрта».

Решение: Используем
классическое определение вероятности:
P=m/n, где m — число исходов, благоприятствующих
осуществлению события, а n — число всех
возможных исходов. 

n
= 5*4*3*2 = 120 способов, так как первую карточку
(букву) можно вытянуть (выбрать) 5 способами
(так как всего карточек пять), вторую —
4 (осталось к этому шагу четыре), третью
— 3 и четвертую — 2 способами. m = 1, так как
искомая последовательность карточек
«ю», потом «р»,
потом «т», потом «а» только одна. 

Получаем P = 1/120. 

Ответ: 1/120.

Задача
9. Ребенок
имеет на руках 5 кубиков с буквами: А, К,
К, Л, У. Какова вероятность того, что
ребенок соберет из кубиков слово «кукла»?

Решение: Используем
классическое определение вероятности:
P=m/n, где n — число всех возможных элементарных
исходов, m — число элементарных исходов,
благоприятствующих осуществлению события. Число
различных перестановок из букв А, К, К,
Л, У равно 
,
из них только одна соответствует слову
«кукла» (m=1), поэтому по классическому
определению вероятности вероятность
того, что ребенок соберет из кубиков
слово «кукла» равна P=1/60. 

Ответ: 1/60.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задание 1

Найти вероятность того, что набран пятизначный номер телефона не содержит цифру 3.

Решение

Обозначим:

А1 – первая цифра не 3.

А2 – вторая цифра не 3.

А3 – третья цифра не 3.

А4 – четвертая цифра не 3.

А5 – пятая цифра не 3.

Тогда первой цифрой может быть любая из 8 цифр (не 0 и не 3), второй-пятой может быть любая из 9 цифр.

То есть:

P(A1)=8/10

P(A2)=9/10

P(A3)=9/10

P(A4)=9/10

P(A5)=9/10

А- набран пятизначный номер телефона не содержит цифру 3.

Р(А)=8/10*9/10*9/10*9/10*9/10=0,52488

В урне 6 белых и 6 черных шариков. Из урны дважды наугад вынимают по одному шарику без возвращения. Найти вероятность появления белого шарика при втором испытании.

Решение

Строим гипотезы:

В1 – первый шарик был белым

В2 – первый шарик был черным

Р(В1)=6/12=0,5

Р(В2)=6/12=0,5

А — появления белого шарика при втором испытании.

Р(А/В1)=5/11

Р(А/В2)=6/11

По формуле полной вероятности:

Р(А)=0,5*5/11+0,5*6/11=0,5

Руководитель пожарной команды собрал статистические данные о количестве по крайней мере одного фальшивого вызова в день за предыдущие 360 дней. Если вероятность по крайней мере одного фальшивого вызова в день равняется 1/6, то какое самое вероятное число таких дней?

Решение

Наивероятнейшее число наступления событий:

Целые число между двумя полученными значениями: n0=60.

Значит, самое вероятное число таких дней: 60.

Из поступающих для составления деталей от станка №1 – 0,1% бракованных, от станка №2 – 0,2%, от станка №3 – 0,25%, от станка №4 – 0,5%. Производительность станков относятся соответственно как 4:3:2:1. Взятая наугад деталь является стандартной. Какая вероятность того, что она изготовлена на станке №3?

Решение

В1 – деталь изготовлена на станке №1

В2 – деталь изготовлена на станке №2

В3 – деталь изготовлена на станке №3

Р(В1)=0,4

Р(В2)=0,3

Р(В3)=0,2

Р(В4)=0,1

А — Взятая наугад деталь является стандартной

Р(В1/А)=1-0,1=0,9

Р(В2/А)=1-0,2=0,8

Р(В3/А)=1-0,25=0,75

Р(В4/А)=1-0,5=0,5

По формуле полной вероятности:

Р(А)=0,4*0,9+0,3*0,8+0,2*0,75+0,1*0,5=0,8

По формуле Байеса, вероятность того, что деталь изготовлена на станке №3:

Р(А/В3)=0,2*0,75/0,8=0,1875.

Задание 2

В урне 4 белых и 3 черных шариков. Проводится последовательное вынимание шариков к появлению черного шарика (выборка осуществляется с возвращением ). Случайная величина Х – число проведенных выниманий. Построить закон распределения случайной величины Х.

Решение

Выборка осуществляется с возвращением, поэтому вероятность изъятия белого шара: р=4/7.

Вероятность изъятия черного шара: q=3/7.

X={1, 2, 3, 4, …, n, ….}

К=1 – при первом изъятии появился черный шар

Р(к=1)=3/7.

К=2 – черный шар появился при втором изъятии

Р(к=2)=4/7*3/7

К=3 – черный шар появился при третьем изъятии

Р(к=3)=4/7*4/7*3/7

…….

К=n – черный шар появился при n изъятии

Р(к=n)=

X	1	2	3	…	N	….
P	3/7	12/49	48/343	…		….

Вероятность попадания в мишень при одном выстреле равняется 0,6. Построить закон распределения случайной величины Х – числа попаданий в мишень, если были сделаны 3 выстрела. Построить многоугольник распределения случайной величины Х.

Решение

Используем формулу Бернулли

Были сделаны 3 выстрела, поэтому число попаданий может быть:

К=0, 1, 2, 3.

Закон распределения:

К	0	1	2	3
Р	0,064	0,288	0,432	0,216

Задание 3

Средний доход на душу населения в размере 8000 грн. считается случайной величиной, которая распределена нормально со средним квадратичным отклонением грн. В каких пределах практически можно гарантировать доход на душу населения с вероятностью 0,9973?

Решение

Среднее: а=8000

Среднеквадратичное отклонение:

По правилу 3 сигм, с вероятностью 0,9973 значение испытания находится в пределах: .

То есть, с вероятностью 0,9973 можно гарантировать доход на душу населения в пределах: (7400; 8600).

Задание 4

Качество продукции контролируется за наличием в ней дефектов двух видов Х и Y. Эти дефекты являются случайными величинами, которые имеют закон распределения, указанный в таблице. Нужно найти:

1) законы распределения компонент Х и Y;

2) условное распределение Y при условии, что Х принимает свое наименьшее значение;

3) ковариацию и коэффициент корреляции дефектов и выяснить зависимые они или нет.

X	Y
4	5	6	7
2	0,1	0,1	0	0
3	0	0,3	0,2	0
4	0	0	0,2	0,1

Решение

1) Закон распределения Х:

Закон распределения У:

У	4	5	6	7
Р	0,1	0,4	0,4	0,1

2) условное распределение Y при условии, что Х принимает свое наименьшее значение:

Х=2

У/х=2	4	5	6	7
Р	0,5	0,5	0	0

3) ковариацию и коэффициент корреляции дефектов и выяснить зависимые они или нет.

Факторы зависимы.

Задание 5

Задана генеральная совокупность, которая характеризует месячную прибыль малых предприятий (в тис. грн.) Сделать выборку из 40 элементов и выполнить такие упражнения:

1) построить статистическое распределение выборки и его эмпирическую функцию распределения;

2) построить интервальное распределение выборки, разбив статистический ряд на 6 ровных подинтервалы;

3) построить полигон частот и гистограмму относительных частот;

4) найти моду, медиану, размах и коэффициент ковариации; Замечание. Выборку осуществлять путем выбора 40 элементов кряду начиная из некоторого N, где N – две последних цифры зачетной книжки. (мои две оследние цифры в зачетке 30)

12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 10, 12, 21, 18, 17, 16, 7, 10, 13, 14, 17, 18, 16, 16, 8, 9,12,16, 21, 17, 19, 15, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16, 16, 21, 17, 15, 14, 12.

Решение

N=30, тридцатое число в ряду: 21.

Получаем выборку:

21, 18, 17, 16, 7, 10, 13, 14, 17, 18, 16, 16, 8, 9,12,16, 21, 17, 19, 15, 14, 17, 18, 16, 16, 8, 11, 15, 19, 21, 9, 12, 10, 7, 10, 13, 14, 17, 18, 16.

1)  построить статистическое распределение выборки и его эмпирическую функцию распределения:

Статистический ряд:

X	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
N	2	2	2	3	1	2	2	3	2	7	5	4	2	0	3

Эмпирическая функция:

X	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
N	2	2	2	3	1	2	2	3	2	7	5	4	2	0	3
Х*	2	4	6	9	10	12	14	17	19	26	31	35	37	37	40

2) построить интервальное распределение выборки, разбив статистический ряд на 6 ровных подинтервалы

Ширина интервала составит:

Xmax — максимальное значение группировочного признака в совокупности.

Xmin — минимальное значение группировочного признака.

Результаты группировки оформим в виде таблицы:

Группы	№ совокупности	Частота fI
7 — 9.33	1,2,3,4,5,6	6
9.33 — 11.66	7,8,9,10	4
11.66 — 13.99	11,12,13,14	4
13.99 — 16.32	15,16,17,18,19,20,21,22,23,24,25,26	12
16.32 — 18.65	27,28,29,30,31,32,33,34,35	9
18.65 — 20.98	36,37,38,39,40	5

3) построить полигон частот и гистограмму относительных частот

4) найти моду, медиану, размах и коэффициент ковариации

Таблица для вычислений:

Группы	Середина интервала, xi	Кол-во, fi	Xi * fi	Накопленная частота, S	(x — xср) * f	(x — xср)2 * f	Частота, fi/n
7 — 9.33	8.17	6	48.99	6	38.1	241.88	0.15
9.33 — 11.66	10.5	4	41.98	10	16.08	64.62	0.1
11.66 — 13.99	12.83	4	51.3	14	6.76	11.41	0.1
13.99 — 16.32	15.16	12	181.86	26	7.69	4.93	0.3
16.32 — 18.65	17.49	9	157.37	35	26.74	79.43	0.23
18.65 — 20.98	19.82	5	99.08	40	26.5	140.49	0.13
суммы		40	580.57		121.86	542.75	1

Средняя взвешенная

Мода

Где x0 – начало модального интервала; h – величина интервала; f2 –частота, соответствующая модальному интервалу; f1 – предмодальная частота; f3 – послемодальная частота.

Медиана

В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Положение медианы определяется ее номером:

Находим середину ранжированного ряда: h = (n+1)/2 = (40+1)/2 = 21.

Медианным является интервал 13.99 — 16.32, т. к. в этом интервале накопленная частота S, больше медианного номера.

Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т. е. отклонения от среднего).

Среднее квадратическое отклонение (средняя ошибка выборки).

Коэффициент вариации — мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Задание 6

Распределение размеров основных производственных фондов (в млн. грн.) на n случайно отобранных предприятиях приведено в таблице. Найти точечные несмещенные оценки для и исправлено среднее квадратичное отклонение.

	11	13	15	17	19	21
	10	8	12	6	14	5

Решение

Таблица для расчета показателей.

Xi	Кол-во, fi	Xi * fi	Накопленная частота, S	(x — xср) * f	(x — xср)2 * f
11	10	110	10	47.64	226.92
13	8	104	18	22.11	61.1
15	12	180	30	9.16	7
17	6	102	36	7.42	9.17
19	14	266	50	45.31	146.64
21	5	105	55	26.18	137.1
сумма	55	867		157.82	587.93

Средняя:

Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т. е. отклонения от среднего).

Исправленная дисперсия:

Среднее квадратическое отклонение (средняя ошибка выборки).

Исправленное среднее квадратическое отклонение:

Задание 7

Провели 15 измерений одним устройством (без систематических ошибок) некоторой физической величины, при этом исправлено среднеквадратичное отклонение S случайных ошибок измерения оказалось ровным 0,12. Найти точность устройства с надежностью 0,99.

Решение

Из равенства

Точность устройства: 9,6%.

Задание 8

По статистическим данным за 10 лет имеет место зависимость валового выпуска продукции предприятия Y от имеющихся основных производственных фондов Х. Дани задаются таблицей

Y = Yi	400-30	420-30	430-30	440-30	450-30	460-30	470-30	480-30	490-30	500-30
X = Xi	150-30	160-30	170-30	180-30	190-30	200-30	210-30	220-30	230-30	240-30

Необходимо:

1) Построить корреляционное поле зависимости признака Х от Y;

2) Основываясь на гипотетическом предположении, что между признаками Х и Y существует линейная зависимость, записать соответствующее уравнение регрессии;

3) Проверить тесноту связи между признаками Х и Y, вычислив коэффициент корреляции;

4) Проверить значимость коэффициента корреляции за критерием Стьюдента.

Решение

Y = Yi	370	390	400	410	420	430	440	450	460	470
X = Xi	120	130	140	150	160	170	180	190	200	210

Линейное уравнение регрессии имеет вид y = bx + a.

Коэффициенты уравнения регрессии находим из системы нормальных уравнений:

A•n + b∑x = ∑y

A∑x + b∑x2 = ∑y•x

Строим вспомогательную таблицу:

X	Y	X2	Y2	X • y
120	370	14400	136900	44400
130	390	16900	152100	50700
140	400	19600	160000	56000
150	410	22500	168100	61500
160	420	25600	176400	67200
170	430	28900	184900	73100
180	440	32400	193600	79200
190	450	36100	202500	85500
200	460	40000	211600	92000
210	470	44100	220900	98700
Сумма 1650	4240	280500	1807000	708300

Для наших данных система уравнений имеет вид

10a + 1650 b = 4240

1650 a + 280500 b = 708300

Из первого уравнения выражаем А и подставим во второе уравнение:

Получаем эмпирические коэффициенты регрессии: b = 1.0545, a = 250

Уравнение регрессии (эмпирическое уравнение регрессии):

Y = 1.0545 x + 250

Параметры уравнения регрессии.

Выборочные средние.

Выборочные дисперсии:

Среднеквадратическое отклонение

Коэффициент корреляции находим по формуле:

Связь очень высокая прямая.

Значимость коэффициента корреляции:

Для того чтобы при уровне значимости α проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины при конкурирующей гипотезе H1 ≠ 0, надо вычислить наблюдаемое значение критерия

И по таблице критических точек распределения Стьюдента, по заданному уровню значимости α и числу степеней свободы k = n — 2 найти критическую точку tкрит двусторонней критической области. Если tнабл < tкрит оснований отвергнуть нулевую гипотезу. Если |tнабл| > tкрит — нулевую гипотезу отвергают.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=8 находим tкрит:

Tкрит (n-m-1;α/2) = (8;0.025) = 2.306

Где m = 1 — количество объясняющих переменных.

Получили, что |tнабл| > tкрит, — коэффициент корреляции статистически значим.

Задание 9

По данному интервальному распределению выборки объема n при уровне значимости а по критерию согласия Пирсона проверить гипотезу о нормальном распределении генеральной совокупности.

	(-4,-1)	(-1,2)	(2,5)	(5,8)	(8,11)	(11,14)
	72	55	37	24	10	2

Решение

Проверим гипотезу о том, что Х распределено по Нормальному закону с помощью критерия согласия Пирсона.

Где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону

Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа

Таблица для расчета показателей.

Группы	Xi	Кол-во, fi	Xi * fi	(x — xср) * f	(x — xср)2 * f
-4 — -1	-2.5	72	-180	271.08	1020.62
-1 — 2	0.5	55	27.5	42.08	32.19
2 — 5	3.5	37	129.5	82.7	184.82
5 — 8	6.5	24	156	125.64	657.73
8 — 11	9.5	10	95	82.35	678.15
11 — 14	12.5	2	25	22.47	252.45
		200	253	626.31	2825.96

Средняя взвешенная

Дисперсия — характеризует меру разброса около ее среднего значения (мера рассеивания, т. е. отклонения от среднего).

Несмещенная оценка дисперсии — состоятельная оценка дисперсии.

Среднее квадратическое отклонение (средняя ошибка выборки).

Каждое значение ряда отличается от среднего значения 1.27 не более, чем на 3.76

Оценка среднеквадратического отклонения.

Интервалы группировки	Наблюдаемая частота ni	Ф(xi)	Ф(xi+1)	Вероятность pi попадания в i-й интервал	Ожидаемая частота npi	Слагаемые статистики Пирсона Ki
-4 — -1	72	0.23	0.42	0.19	38.02	30.37
-1 — 2	55	0.0793	0.23	0.15	29.96	20.93
2 — 5	37	0.34	0.0793	0.26	52.4	4.53
5 — 8	24	0.46	0.34	0.12	24.4	0.0065
8 — 11	10	0.5	0.46	0.032	6.4	2.03
11 — 14	2	0.5	0.5	0.00436	0.87	1.46
сумма	200					59.31

Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.

Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).

Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).

Kkp = 9.34840; Kнабл = 59.31

Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены Не по нормальному закону.

< Предыдущая		Следующая >

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям