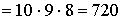поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,612 -
гуманитарные
33,644 -
юридические
17,916 -
школьный раздел
611,418 -
разное
16,896
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Набирая номер телефона, абонент забыл последние 3 цифры и, помня, что эти цифры различные, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Классическое определение вероятности
Вероятностью события А называют отношение m на n и определяется по формуле: 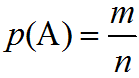
m — числа всех благоприятных комбинаций этому событию исходов эксперимента;
n — общее число всех возможных исходов эксперимента.
Вероятность события А обозначается Р(А) .
Основные понятия классической теории вероятности и свойство вероятности рассмотрено здесь.
Рассмотрим примеры, основанные на классическом определение вероятностей.
Пример 1
В урне 10 красных и 8 синих шаров. Наугад вынимают один. Какова вероятность того, что вынут шар красного цвета?
Решение
Пример 2
В урне 2 белых и 5 черных шаров. Из урны вынимают один шар и откладывают в сторону. Этот шар оказался белым. После этого из урны берут еще один шар. Найти вероятность того, что этот шар тоже будет белым.
Решение
Пример 3
Игральная кость бросается один раз. Найти вероятность следующих событий:
А1 — появление нечетного числа очков;
A2 — появление не менее 3 очков;
A3 — появление не более 5 очков.
Решение
- Возможные варианты выпадения очков при одном бросании кости: 1, 2, 3, 4, 5, 6. Нечётные — 1, 3, 5. Тогда вероятность равна:
2. Появление не менее 3 очков — это очки: 3, 4, 5, 6, следовательно
3. Появление не более 5 очков — это очки: 1, 2, 3, 4, 5, тогда имеем
Пример 4
Монета брошена два раза. Найти вероятность того, что хотя бы один раз появился «герб».
Решение
Найдем все комбинации n подбрасывания монеты два раза, имеем:
«решка» — «герб»
«герб» — «решка»
«решка» — «решка»
«герб» — «герб»
Составим все комбинации события m А — «при бросании монеты два раза хотя бы один раз появился герб»
«решка» — «герб»
«герб» — «решка»
«герб» — «герб»
Пример 5
Бросаются одновременно две игральные кости. Найти вероятности следующих событий:
- А1 — сумма выпавших очков равна 9;
2. A2 — произведение выпавших очков равно 6;
3. A3 — сумма выпавших очков больше 4.
Решение
Составим всевозможные комбинаций, при которых сумма очков двух игральных костей равна 9
| Первая кость | Вторая кость |
| Три | Шесть |
| Шесть | Три |
| Пять | Четыре |
| Четыре | Пять |
Итак, m=4
Общее количество комбинаций равно
n=6·6=36
2. Составим таблицу, при котором произведение выпавших очков равно 6;
| Первая кость | Вторая кость |
| Три | Два |
| Два | Три |
| Шесть | Один |
| Один | Шесть |
m=4, n=6·6=36
$p() = frac= frac = frac$
3. Чтобы найти сумму выпавших очков больше 4, сначала найдём сумму очков, которая меньше 4, для этого составим таблицу
| Первая кость | Вторая кость |
| Один | Два |
| Два | Один |
| Один | Один |
| Два | Два |
| Один | Три |
| Три | Один |
m=36-6=30, n=6·6=36
Найдем событие A3 — сумма выпавших очков больше 4
Пример 6
В коробке 6 одинаковых, занумерованных кубиков. Наудачу по одному извлекают все кубики. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Решение
Событие «номера извлеченных кубиков появятся в возрастающем порядке» может произойти в одном случае, то есть m=1.
По формуле комбинаторики перестановка без повторений найдем число комбинаций извлечения шести кубиков
$n = = 6! = 1cdot2cdot3cdot4cdot5cdot6 = 720$
Вероятность извлеченных кубиков в возрастающем порядке равна:
Пример 7
Набирая номер телефона, абонент забыл последние три цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры
Решение
А — «абонент набрал нужные три цифры»
m — число благоприятных комбинаций событию А — одно;
n — число комбинаций, которыми можно набрать три цифры и вычисляется по формуле размещение без повторения, тогда
Пример 8
В пачке 20 перфокарт, помеченных номерами 101, 102, … , 120 и произвольно расположенных. Перфораторщица наудачу извлекает две карты. Найти вероятность того, что извлечены перфокарты с номерами 101 и 120.
Решение
Событие А — «перфораторщица наудачу извлекает две карты с номерами 101 и 120».
Общее число комбинаций выбора 2-ух карт из 20 равно:
$C_^2 = frac>> = frac>> = 190$
Количество благоприятных комбинаций событию А — одно, получаем
$Pleft( A right) = frac^2>> = frac>$
Пример 9
В ящике 10 деталей, из которых четыре окрашены. Сборщик наудачу взял три детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
Решение
А — «хотя бы одна из взятых деталей окрашена»
Событие A может произойти в трёх случаях:
«одна деталь окрашена», «две детали окрашены», «три детали окрашены»
Противоположное событие $overline A $ событию A, это «все три детали не окрашены», получаем вероятность
А противоположное событие исходя из условия задачи находится по формуле
Общее число исходов извлечённых из ящика четыре окрашенных деталей из десяти равно
$m = $C_^4$
Число извлечённых из ящика трех деталей из десяти
$m = $C_^4$
Пример 10
В урне 3 белых и 7 черных. Из урны вынимают сразу два шара. Найти вероятность того, что оба шара будут белыми.
Решение
Пусть событие A — вероятность того, что оба шара будут белыми.
Найдем общее число случаев по формуле сочетание без повторений
Количество благоприятных случаев выбора двух белых шаров из трёх равно
Получаем решение, воспользовавшись общей формулой теории вероятностей
Пример 11
В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает три детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
Решение
А — «три извлеченные детали сборщиком окажутся окрашенными».
Здесь,
m— количество комбинаций извлечения трех окрашенных деталей из десяти;
n— общее число извлечения трех деталей из пятнадцати.
Пример 12
Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
Решение
А — «студент знает предложенные ему экзаменатором три вопроса»
Пример 13
В коробке 5 белых и 7 красных шара. Из нее одновременно наугад вынимают два шара. Найти вероятность того, что они разного цвета.
Решение
$n = C_^2$
$m = C_5^1 cdot C_7^1$
Через формулу комбинаторики сочетание без повторений, найдём вероятность вынуть шары разных цветов (один красный и один белый шар), равна
Пример 14
На складе имеется 15 кинескопов, причем 10 из них изготовлены Львовским заводом. Найти вероятность того, что среди пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода
Решение
А — «из пяти взятых наудачу кинескопов окажутся три кинескопа Львовского завода».
Число способов выбрать три кинескопа Львовского завода из десяти кинескопов Львовского завода равно $C_^3$
Число способов выбрать два кинескопа, которые не изготовлены Львовским заводом из пяти равно $C_^2$
Таким образом
$m = C_^3 cdot C_5^2$
Число комбинаций, которыми можно выбрать пять кинескопов из пятнадцати
$n=C_^5$
Следовательно,
Пример 15
Устройство состоит из пяти элементов, два из которых изношены. При включении устройства включаются случайным образом два элемента. Найти вероятность того, что включенными окажутся неизношенные элементы.
Решение
$Pleft( A right) = frac>> = frac> = 0,3$
Пример 16
В коробке пять одинаковых изделий, причем три из них окрашены. Наудачу извлечены два изделия. Найти вероятность того, что среди двух извлеченных изделий окажутся:
1) одно окрашенное изделие;
2) два окрашенных изделия;
3) хотя бы одно окрашенное изделие.
Решение
1) А — «среди двух извлеченных изделий окажется одно окрашенное изделие»
Число способов выбрать одно изделие из трех окрашенных изделий $C_^1$
Неокрашенное изделие можно выбрать $C_^1$
тогда m равно
$m = $C_^1 cdot C_^1$
Общее число способов, которыми можно выбрать два изделия из пяти равно
$n=C_^2$
Имеем,
2) В — «два извлеченных изделия окрашены»
Число комбинаций извлечения двух окрашенных изделий $m = $C_^2$
Общее число комбинаций извлечения два изделия из пяти $n=C_^2$
3) С — «извлечено хотя бы одно окрашенное изделие»
Число благоприятных способов извлечения двух изделий нет двух неокрашенных соответствует единице. Тогда:

Вычисление вероятности по классической формуле
n-число всех возможных элементарных исходов испытания.
Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.16. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.
Решение: Введем события: – одно очко; — два очка; – три очка; – четыре очка; – пять очков; – шесть очков. Итак, n=6.
Рассмотрим событие A — выпадение четного числа очков. Данному событию благоприятствуют элементарные исходы , , .
Следовательно, m=3. Тогда .
ПРИМЕР 13.2.17. Набирая номер телефона, абонент забыл последние три цифры и помнит лишь то, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение: Событие A — набраны нужные цифры.
n — общее число элементарных исходов опыта равно
m=1, так как единственная комбинация цифр благоприятствует событию A. Тогда .
ПРИМЕР 13.2.18. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 6 отличников.
Решение: Событие A- среди отобранных студентов окажутся 6 отличников. Число n равно числу способов, которыми можно отобрать 9 студентов из 12
Подсчитаем число исходов, благоприятствующих появлению события A. Из 8 отличников 6 можно отобрать способами. Отобрать нужно 9 человек, остальных 3 отбираем среди неотличников. Их всего 12-8=4. Троих студентов-неотличников из четырех можно отобрать способами. По теореме умножения комбинаторики . Тогда,
Примеры и задачи для самостоятельного решения
Решить задачу, используя формулу классической вероятности
13.2.2.1. В урне белых, черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.
13.2.2.2. Брошены две игральные кости. Найти вероятность того, что сумма очков четная, причем на грани хотя бы одной из костей появится шестерка.
13.2.2.3. В ящике 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
13.2.2.4. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три.
Отв.:а)0,384; б)0,096; в)0,008
13.2.2.5. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем; б) не есть дубль.
Отв.: а) 2/9; б) 4/9
13.2.2.6. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное число; б) случайно названное число, цифры которого различны.
Отв.:а) 1/90;б) 1/81
13.2.2.7. Из пяти букв разрезной азбуки составлено слово «ягуар». Ребенок не умеющий читать, рассыпал карточки с буквами и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получится слово «ягуар».
13.2.2.8. В условиях предыдущей задачи найти вероятность, если ребенок играл со словами: а) молоко; б) шалаш.
Отв.: а)1/120; б)1/30
13.2.2.9. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.
13.2.2.10. В мастерскую для ремонта поступили 10 часов. Известно, что 6 штук из них нуждаются в общей чистке механизма. Мастер берет первые попавшиеся 5 часов. Определить вероятность того, что двое из этих часов нуждаются в общей чистке механизма.
13.2.2.11. Из партии, в которой 31 деталь без дефектов и 6 с дефектами, берут наудачу 3 детали. Чему равна вероятность в следующих случаях: а) все три детали без дефектов; б) по крайней мере, одна деталь без дефектов?
Отв.:a)0,579; б)0,9973
13.2.2.12. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
13.2.2.13. Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.
13.2.2.14. Найти вероятность выигрышных комбинаций в популярной спортивной лотерее «5 из 36».
Отв.: 1/376992; 155/376992; 775/62832
13.2.2.15. Найти вероятность того, что наудачу выбранное двузначное число делится на 8.
Уважаемые студенты
На нашем сайте можно получить помощь по всем разделам математики и другим предметам:
✔ Решение задач
✔ Выполнение учебных работ
✔ Помощь на экзаменах
|
0 / 0 / 0 Регистрация: 21.01.2014 Сообщений: 35 |
|
|
1 |
|
Набирая номер телефона, абонент забыл три последние цифры20.03.2014, 20:32. Показов 21314. Ответов 3
Набирая номер телефона, абонент забыл три последние цифры и, помня лишь, что эти цифры различны, набрал их на удачу. Найти вероятность того, что набраны нужные цифры.
__________________
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
20.03.2014, 20:32 |
|
3 |
|
831 / 678 / 101 Регистрация: 11.11.2012 Сообщений: 1,796 |
|
|
20.03.2014, 21:43 |
2 |
|
Решение сколько комбинаций из трех различных цифр? Это будет N ПО классическому определению Р(А)=M/N
2 |
|
0 / 0 / 0 Регистрация: 21.01.2014 Сообщений: 35 |
|
|
20.03.2014, 21:45 [ТС] |
3 |
|
Спасибо огромное за обьяснение
0 |
|
831 / 678 / 101 Регистрация: 11.11.2012 Сообщений: 1,796 |
|
|
20.03.2014, 21:58 |
4 |
|
Только N давайте обсудим еще. а то ответа-то нет! Добавлено через 2 минуты Или просто использовать число размещений из 10 цифр по 3 (т.к. цифры не должны повторяться)
0 |
Рассмотрим
множество, состоящее из n
различных элементов. Требуется выбрать
из них какие-нибудь k
элементов
и расположить их в каком-нибудь порядке.
Такие упорядоченные последовательности
называются размещениями
из n
элементов по k
элементов.
Если
в последовательности нет одинаковых
элементов, то говорят о размещении
без повторений.
Их количество:
Если
в последовательности допускается
наличие одинаковых элементов, то говорят
о размещении
с повторением.
Их количество:
Любое
множество (неупорядоченное), состоящее
из k
элементов, называется сочетанием
из n
элементов по k
элементов. Различные сочетания отличаются
друг от друга только самими входящими
в них элементами, порядок их следования
безразличен.
Число
сочетаний
без
повторений:
Число
сочетаний
с повторениями:
.
Количество
способов переставить n
элементов в заданном множестве –
количество перестановок
вычисляется по формуле:
Рассмотрим
следующие примеры:
ПРИМЕР1.1.
В коробке 6 шаров, пронумерованных от
1 до 6. Из коробки вынимают друг за другом
3 шара и в том же порядке записывают
полученные цифры. Сколько трехзначных
чисел можно таким образом записать?
Решение:
По условию задачи подмножества
и
— различные. Повторов в подмножестве
быть не может, так как шары не возвращаются
в коробку.n
= 6, k
= 3.
ПРИМЕР
1.2. В
коробке 6 шаров, пронумерованных от 1 до
6. Из коробки вынимают друг за другом 3
шара и записывают число в порядке
возрастания цифр. Сколько трехзначных
чисел можно таким образом записать?
Решение:
По условию задачи подмножества
и
дают число 123, т.е. не являются различными.
.
ПРИМЕР
1.3. Условие
задачи 1.1 (шары возвращаются в коробку).
Решение:
.
ПРИМЕР1.4.
Условие задачи 1.2 (шары возвращаются в
коробку).
Решение:
.
ПРИМЕР
1.5. Сколько
различных перестановок можно составить
из букв слова «весна»?
Решение:
.
ПРИМЕР
1.6. Сколько
различных перестановок можно составить
из букв слова «задача»?
Решение:
Если бы все шесть букв слова были
различны, то число перестановок было
бы 6! Но буква «а» встречается в данном
слове три раза, и перестановки только
этих трех букв не дают новых способов
расположения букв. Поэтому число
перестановок букв слова задача будет
не 6!, а в 3! раза меньше, т.е.
.
2. Вычисление вероятности по классической формуле
Вероятность события
А определяется формулой

где
m
— число элементарных исходов,
благоприятствующих событию А; n
— число всех возможных элементарных
исходов испытания.
Предполагается,
что элементарные исходы несовместны,
равновозможны и образуют полную группу.
ПРИМЕР 2.1.
Брошена игральная кость. Найти вероятность
того, что выпадет четное число очков.
Решение:
Введем события: E1—
одно очко; E2
— два очка, E3—
три очка; E4—
четыре очка; E5
— пять очков; E6—
шесть очков. Итак, n
= 6.
Рассмотрим событие
А — выпадение четного числа очков. Данному
событию благоприятствуют элементарные
исходы E2,
E4,
E6.
Следовательно,
m
= 3. Тогда
ПРИМЕР 2.2.
Набирая номер телефона, абонент забыл
последние три цифры и помнит лишь то,
что эти цифры различны, набрал их наудачу.
Найти вероятность того, что набраны
нужные цифры.
Решение:
Событие А — набраны нужные цифры, n
— общее число элементарных исходов опыта
равно
.
m
= 1, так как единственная комбинация цифр
благоприятствует событию А. Тогда

ПРИМЕР 2.3.
В группе 12 студентов, среди которых 8
отличников. По списку наудачу отобраны
9 студентов. Найти вероятность того, что
среди отобранных студентов окажутся 6
отличников.
Решение:
Событие А — среди отобранных студентов
окажутся 6 отличников. Число n
равно числу способов, которыми можно
отобрать 9 студентов из 12.
Подсчитаем
число исходов, благоприятствующих
появлению события А. Из 8 отличников 6
можно отобрать
способами.
Отобрать нужно 9 человек, остальных 3
отбираем среди неотличников. Их всего
12-8=4. Троих студентов-неотличников из
четырех можно отобратьспособами. По теореме умножения
комбинаторики.
Тогда
Вероятность события A определяется формулой
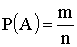
где m-число элементарных исходов, благоприятствующих событию A ;
n-число всех возможных элементарных исходов испытания.
Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.16. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.
Решение: Введем события: 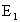
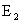
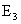
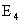
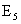
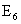
Рассмотрим событие A — выпадение четного числа очков. Данному событию благоприятствуют элементарные исходы 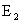
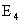
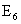
Следовательно, m=3. Тогда 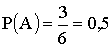
ПРИМЕР 13.2.17. Набирая номер телефона, абонент забыл последние три цифры и помнит лишь то, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение: Событие A — набраны нужные цифры.
n — общее число элементарных исходов опыта равно
m=1, так как единственная комбинация цифр благоприятствует событию A. Тогда .
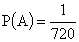
ПРИМЕР 13.2.18. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 6 отличников.
Решение: Событие A- среди отобранных студентов окажутся 6 отличников. Число n равно числу способов, которыми можно отобрать 9 студентов из 12
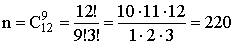
.
Подсчитаем число исходов, благоприятствующих появлению события A. Из 8 отличников 6 можно отобрать 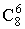
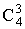
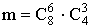
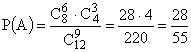
Примеры и задачи для самостоятельного решения
Решить задачу, используя формулу классической вероятности
13.2.2.1. В урне белых, черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.
Отв.:a/(a+b)
13.2.2.2. Брошены две игральные кости. Найти вероятность того, что сумма очков четная, причем на грани хотя бы одной из костей появится шестерка.
Отв.:5/36
13.2.2.3. В ящике 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.
Отв.:0,1
13.2.2.4. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три.
Отв.:а)0,384; б)0,096; в)0,008
13.2.2.5. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем; б) не есть дубль.
Отв.: а) 2/9; б) 4/9
13.2.2.6. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное число; б) случайно названное число, цифры которого различны.
Отв.:а) 1/90;б) 1/81
13.2.2.7. Из пяти букв разрезной азбуки составлено слово «ягуар». Ребенок не умеющий читать, рассыпал карточки с буквами и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получится слово «ягуар».
Отв.: 1/120
13.2.2.8. В условиях предыдущей задачи найти вероятность, если ребенок играл со словами: а) молоко; б) шалаш.
Отв.: а)1/120; б)1/30
13.2.2.9. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.
Отв.: 1/7776
13.2.2.10. В мастерскую для ремонта поступили 10 часов. Известно, что 6 штук из них нуждаются в общей чистке механизма. Мастер берет первые попавшиеся 5 часов. Определить вероятность того, что двое из этих часов нуждаются в общей чистке механизма.
Отв.: 5/21
13.2.2.11. Из партии, в которой 31 деталь без дефектов и 6 с дефектами, берут наудачу 3 детали. Чему равна вероятность в следующих случаях: а) все три детали без дефектов; б) по крайней мере, одна деталь без дефектов?
Отв.:a)0,579; б)0,9973
13.2.2.12. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.
Отв.: 1/4
13.2.2.13. Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.
Отв.:1/3
13.2.2.14. Найти вероятность выигрышных комбинаций в популярной спортивной лотерее «5 из 36».
Отв.: 1/376992; 155/376992; 775/62832
13.2.2.15. Найти вероятность того, что наудачу выбранное двузначное число делится на 8.
Отв.:11/90
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

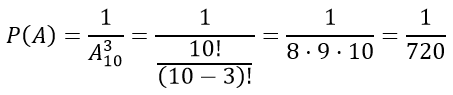
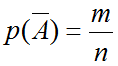
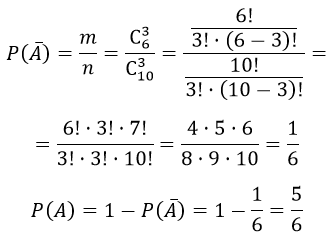
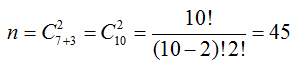
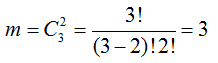
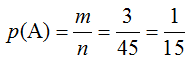
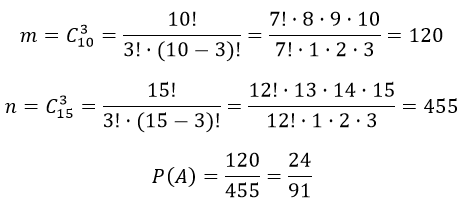
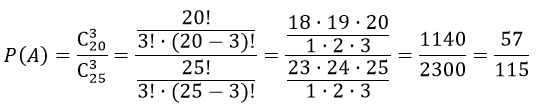
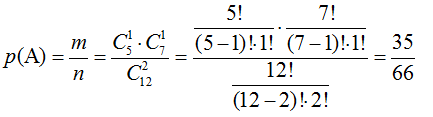
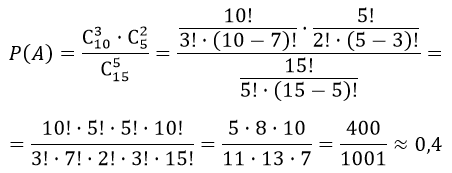
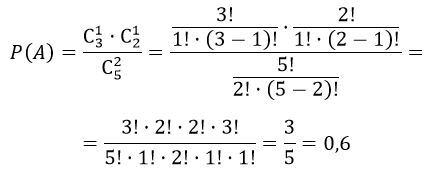
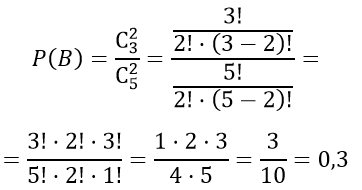
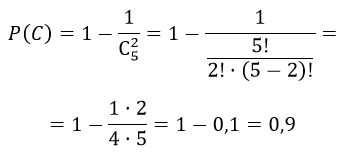

 Сообщение было отмечено NEA3SW как решение
Сообщение было отмечено NEA3SW как решение